野马优化器算法

开始

  还记得那是一个普通的周末，为了应付老师的要求，不得不重新去看新的算法论文，然后就看到了这个野马优化器算法，2021年提出的，也算是一种缘分吧。

引言

  算法由Iraj Naruei等人于2021年提出，主要模拟了野马种群的放牧、交配、领导者的交流和选择这三种行为。因其在CEC2017、CEC2019等测试函数上具有较好的实验结果，而在未来具有广泛的应用前景。

  总体来说，马可以根据其社会组织（领土和非领土）分为两类，在本篇文章，我们重点在于非领土类，它们是由稳定的家庭群体或后宫组成的马群，如小马驹、种马和母马。种马和母马都生活在一起，并在放牧中相互影响。同时为了防止乱伦，小马驹长大后必须离开他们的群体，加入其他群体建立自己的家庭。野马优化器就是使用放牧、交配、领导者的交流和选择这三种行为对问题进行优化。

主要步骤及过程

1. 创建初始种群并形成马群并选择领导者； 2. 马的放牧行为； 3. 马的交配行为； 4. 由领导（种马）领导和领导小组； 5. 领导交流和选拔。

创建初始种群

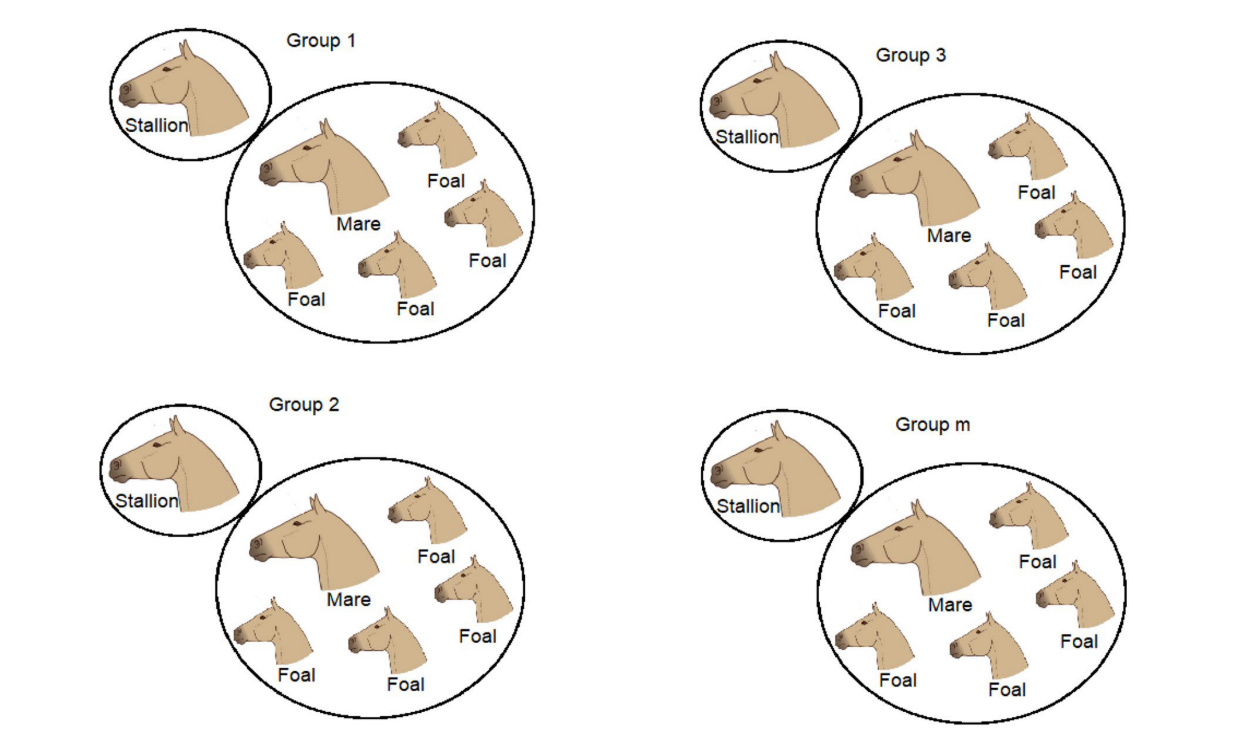
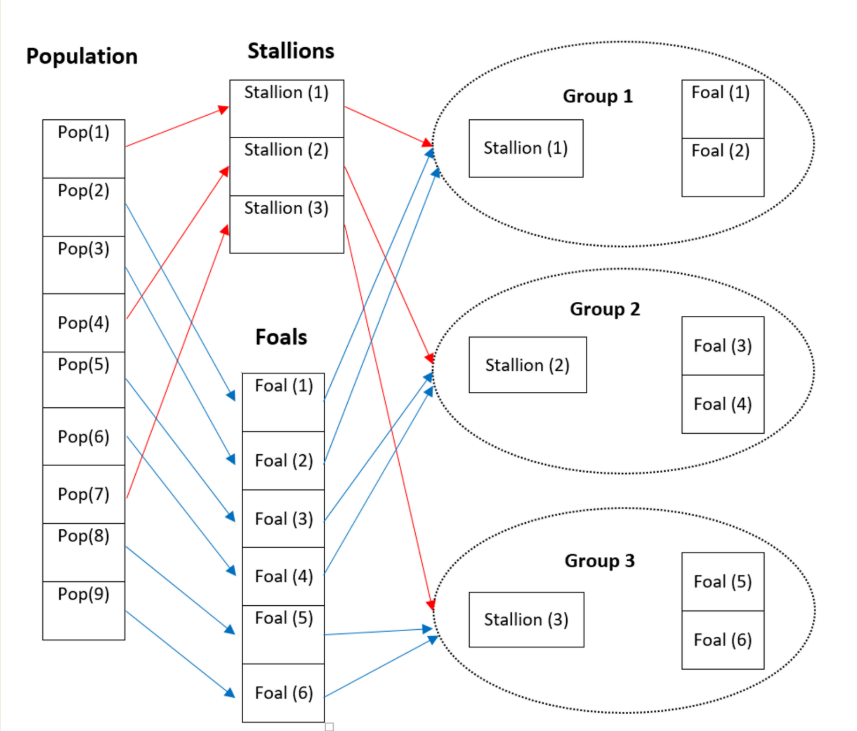
  对初始马群进行分组，如果N是总体的成员数，则组数为是G=[N×PS]. PS 是总种群中种马的百分比。所以我们根据组的数量分出领导者G（种马），其余成员（N - G），在这些组中平均分配。在算法开始时随机选择组的领导者，在后期阶段，根据组成员之间的适应度（最佳适应度函数）来选择他们。 种群初始化示意图 原始种群形成群体的过程图

放牧行为

  如上一节所述，小马驹通常大部分时间都在他们的群体周围吃草。为了实现放牧行为，我们将种马视为放牧区的中心，群体成员在中心周围搜索（放牧）： \[ X_{G, j}^{i}=2 Z \cos (2 \pi R Z) \times\left(\text { Stallion }_{G, j}-X_{G, j}^{i}\right)+\text { Stallion }_{G, j} \]   式中Stallion为领导者的位置，R 为[-2,2]内的随机数，主要控制个体与领导者间的角度，自适应机制Z 的计算方式为：

\[ P=\vec{R} 1<T D R, I D X=(P==0) ; \quad Z=R 2 \Theta I D X+\vec{R} 3 \Theta(\sim I D X) \]

  其中P 是由0和1组成的向量，R1、R3均为[0,1]范围内均匀分布的随机向量，R2为[0,1]内一随机值。满足条件(P==0)的随机向量R1返回的IDX索引。Θ这个符号即点乘。TDR为由1线性递减至0的系数：

\[ TDR=1-iter\times （\frac{1}{maxiter} ） \]

其中iter为当前迭代次数，maxiter为最大迭代次数。

交配行为

  与其他动物相比，马的独特行为之一是将小马驹从群体中分离出来并与它们交配的行为。小马驹在青春期前离开这个群体，雄性小马驹加入单身马群，雌性小马驹加入另一个家庭群体，以达到青春期并寻找配偶。为了模拟马的交配行为，使用公式：

\[ X_{G, k}^{p}=\operatorname{Crossover}\left(X_{G, i}^{q}, X_{G, j}^{z}\right), i \neq j \neq k, q=z=\text { end } \]

  这里Xp_G_K表示种群k中个体p离群后再次进入种群k的个体位置，所以很明显，后面括号里的两个位置即为其父母的位置。可以看出，此阶段主要针对种群内适应度值最差的个体进行操作，目的即为提升种群多样性。

集团领导

  领导者（种马）将带领其他组成员到合适的区域（水坑）。领导者（种马）也将争夺水坑，带领优势组首先使用水坑，直到优势组离开，其他组才能使用水坑。用公式模拟此行为：

\[ \overline{\text { Stallion }} G, j=\left\{\begin{array}{l}2 Z \cos (2 \pi R Z) \times\left(W H-\text { Stallion }_{G, j}\right)+W H, \text { rand }>0.5 \\ 2 Z \cos (2 \pi R Z) \times\left(W H-\text { Stallion }_{G, j}\right)-W H, \text { rand } \leq 0.5\end{array}\right. \]

  式中WH为栖息地的位置(也就是当前最优个体位置)，R、Z 的定义与前文相同。下图展示了领导者相对于栖息地的位置更新过程：

领导者相对于栖息地的位置更新

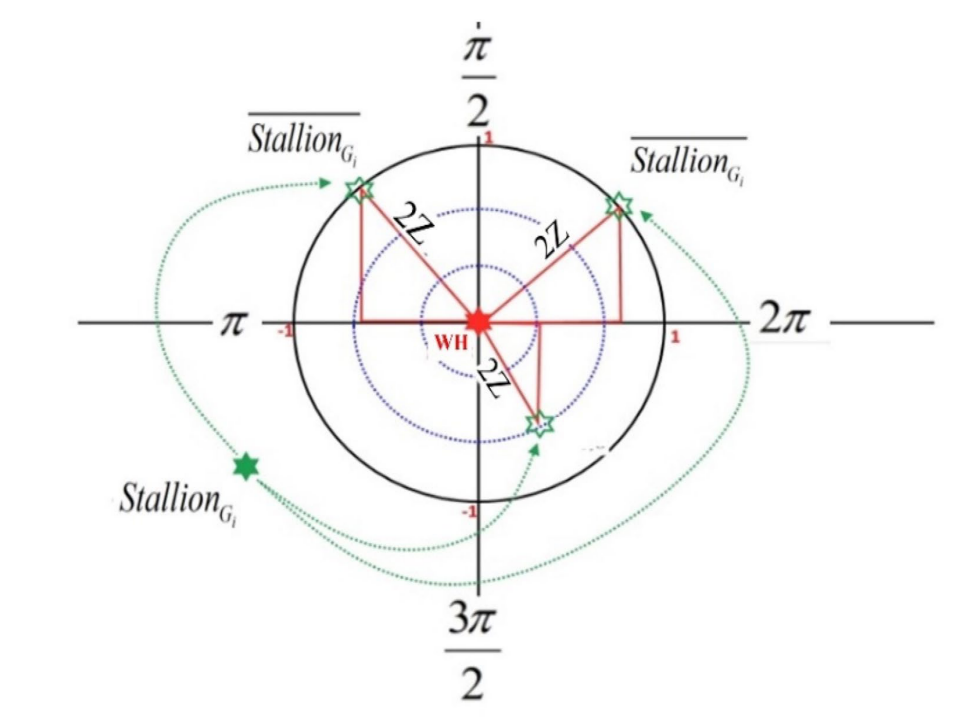
领导交流与选拔

  在开始，领导者是随机选择的。之后，比较组中马驹的适应度值选择领导者。为了模拟领导交流与选拔，使用了公式：

\[ \mathrm{Stallion} _{G,j}=\begin{cases} X_{G,j} & \text{ if } cost(X_{G,j})< cost({Stallion} _{G,j})\\ {Stallion} _{G,j}& \text{ if } cost(X_{G,j})> cost({Stallion} _{G,j}) \end{cases} \]

此处cost函数为适应度函数，算法伪代码如下： 伪代码

总结

  总体来说，野马优化器考虑的较为全面，涉及了精英引导、分群探索、群间交流等方面。不过从测试中来看其跳出局部最优值的能力仍有待提高。对于数据集的处理仍存在较大问题，迭代后期容易陷入局部极值的问题。